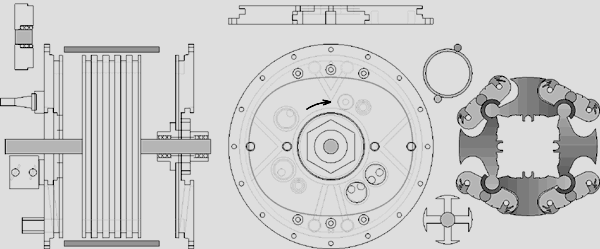
Quasiturbine Continuous Combustion Rotary Engine
Characteristics, torque,
power and consumption
What would you say about a gazoline engine having :
- The noise is 20 times less, because the conventional cubic capacity is divided into 4
or 8, and that the relaxation of gas is more complete, and that there is less of waste
heat to the exhaust.
- The vibrations are comparable with those of an electric motor, and higher accelerations.
- The density of power per volume and unit of weight is 4 times better than that of the of
the same piston engines power because of continuous combustion, and this without
crankshaft nor wheel of inertia.
- The energy effectiveness is higher for 3 reasons: No driving accessory, such eccentric
trees, stems push rods...; The shorter pressure impulse makes it possible to reduce the
heat flow towards the driving block at the time of the relaxation; The zone of lengthened
relaxation allows a better extraction of mechanical energy...
- The production of the NOx pollutants is (estimated at 500 times) less than
those of the pistons, because of the short impulse of pressure which limits the time of
containment, and prevent the start up of NOx reactions.
- Le régime ralenti est 150 rpm, le maximum 3000 rpm. Cette gamme de révolution signifiant aussi une plus grande durabilité temporelle.
- L'ingéniosité le rend en plus ... compatible à l'hydrogène, dans les dispositifs hybrides de demain.
This is the Quasiturbine, an universal engine in relation to energy sources : Liquid and gaseous fuel, hydrogen, steam, pneumatic, hydraulic...
Brief comparison : Piston - Wankel - Quasiturbine
From the numerous criteria permitting to compare engines between themselfs, one
can not ignore the integrity of the expansion volume, and the propulsive factor ratio. One
must recall that all volumes are generated from a surface movement (the cube is generated
by the movement of a square, the cylinder by the movement of a circle), and in order to
get an optimum geometric efficiency, the expansion volume must be generated only by the
effective gas pushing surface. The propulsive factor ratio is the percentage of time (or
of angle) during which the component contribute positively to the engine propulsion.
The integrity of the expansion volume is the implacable characteristic of the piston engine, which has allow it to resist for more than a century to all other engine concept. In fact, lets consider a cylinder with multiple internal cavities perforation (let say for example that the total volumes of all the cavities is twice the volume of the considered cylinder) and in which a piston moves. Since the pushing stroke goes from the minimal volume (top center) to the maximum volume (bottom center), the maximum volume would not be the one generated by the movement of the circular moving piston, i.e.1 cylinder, but 3 time more due to lateral cavities, which would also be responsible for a substantial pressure lost. Such an engine would still run fine, however its energy efficiency would be poor. The conventional piston has a low propulsive factor ratio (120 / 720 degrees = 17%), but a final expansion volume strictly equal to the one generated by the movement of its piston surface, which guaranty a good geometric efficiency.
What about the Wankel ? Since its rotor has only 3 times 30 degrees of dead time per revolution, the propulsive factor ratio reaches (270 / 360 degrees) 75% for the Wankel, which is a substantial improvement. However, the Wankel has several theoritical deficiencies, see http://quasiturbine.promci.qc.ca/QTpasWankel.html . Consequently, the Wankel can not have an energy efficiency as good as the piston engine.
And the Quasiturbine ? Since at the end of each expansion stroke, the following stroke is ready to fired, the dead time is reduced to zero, and the propulsive factor ratio of the Quasiturbine is 100% (continuous combustion). Furthermore, as the confinement contour has been carefully selected such that the final expansion volume is strictly equal to the volume generated by the movement of the variable tangential pushing surface, the geometric efficiency is identical to the piston. In order to get this double optimum, the Quasiturbine does not use the principle of the volume trapped between a variable curvature surface and a fix cord, but rather uses a complete degree of freedom rotor confined into a housing contour shaped as a skating rink, which furthermore allow an optimum torque on a wide angular displacement, and the suppression of the crankshaft and the flywheel.
Bref description :
The invention is a new hybrid engine concept, mid-way between the piston
and the turbine engine.
The concept incorporates the following characteristics:
1 Stator with covers
4 rotative blades
4 rocking carriages
8 wheels
Joints
Furthermore, it:
Uses a conventional carburetor or a non synchronized injector
Can be started with compressed air
Can be used in submerged environments
Has potential for high reliability
Can be produced at a competitive price
We also run our prototype on steam or pressurized air, or fluid flow, and
also as a compressor.
Very large units (well over 1000 HP) are very feasible.

1999 Prototype data :
Diam. max. = 5.57"
Thickness = 2.00"
Aspirated volume =200 cc per revolution
Average pressure 120 lbs/sq.in (not actually measured)
Rated speed: 3000 RPM
(Please do not rate maximum < Shaft Power > at more than 3000 RPM
for small engine, and much less for larger engine)
(Note that theoretically, the rotor perimeter would reach sound speed in atmospheric air
at about 30,000 RPM, which is far from 3000 expected)
(Note: 1 lbforce = 4.44 N; 1 foot = 0.303 m; 1 H.P. = 746 watts)
A - Internal combustion - Power through pressure calculation :
The average torque < Torque > on a complete rotation
is proportional to the average pressure in the engine.
The average torque < Torque > is given by (one chamber pressurized):
< Torque > = 4.84 X < Engine thickness (cm)> X < Diam. max (cm)>**2 X < average Pressure
(bar) >
And the shaft power is (in all unit system): < Shaft Power >
proportional to < RPM/60 > X < Torque >
English: HP = T (lb.in.) x S (RPM) x .0000159
Metric: HP = T (kg.cm.) x S (RPM) x .0000138
SI: HP = T (N.m.)
x S (RPM) x .00014
Watts = HP x 746
Applied to the 1999 prototype case (1 pressurized chambers at 8 bar = 125 psi
average at 3000 RPM) :
< Torque > = 35 N-m or 25 lb-ft
For a < Shaft power > in the range of 14.0 HP or 10.5 kW
B - Internal combustion - Power through consumption calculation :
A 200 cc/rev aspirated volume require about 0,0224 cc/rev of gasoline.
At 3000 rpm => 0,0224 * (3000/60) = 1.12 cc/s of gasoline.
Assuming 32,4 kj/cc as heat power of commercial gasoline,
the maximum heat power that comes from the combustion of 1.12 cc/s is:
1.12cc/s * 32,4 = 36.3 Kw (thermal)
or
29% * 36.3 Kw = 10.5 Kw (mechanical) or
14.0 HP
BSFC (Brake specific fuel consumption) will be at worst:
= (1.12 cc/s) /
(10.5Kw) = 0.107 cc/s-Kw (of gasoline)
or, = 0.107 * 0.746
= 0.080 cc/s-HP (of gasoline)
Which is close to
260 gr / kW-h.
(This at only 3000 RPM. In most applications you can almost forget
the gearbox !).
As a general thumbs rule, internal combustion Quasiturbine power is about 1 / 8
of the power
produced by external pressurized fluids given on this graph:
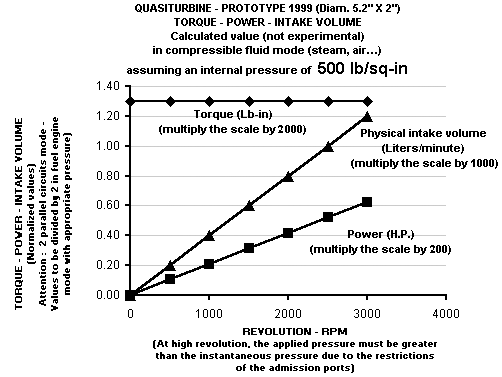
Assuming a pressure differential of 500 lb/sq.in., this graph gives for each rpm
:
the engine torque, the power and the geometric intake flow.
Those result can be scaled linearly for other pressure differentials.
C - For a calculated comparison with the Mazda RX7
Wankel engine, refer to the section :
Why the Quasiturbine is not a Wankel's type engine ?
http://quasiturbine.promci.qc.ca/QTpasWankel.html
| Return to main menu |
Quasiturbine Agence Inc., Promotional
Agent for the Quasiturbine Continuous Combustion Rotary Engine or Compressor
Casier 2804, 3535 Ave Papineau, Montréal Québec H2K 4J9 CANADA (514) 527-8484 Fax (514)
527-9530
http://quasiturbine.promci.qc.ca
quasiturbine@promci.qc.ca